Rangkuman Materi| Tugas 1 dan Tugas 2| Pertemuan ke-1| 25 September 2025

RANGKUMAN MATERI 25 SEPTEMBER

Logika matematika dipelajari untuk membantu manusia mengambil keputusan, karena dalam hidupnya manusia sering membuat keputusan berdasarkan fakta.

---

Kalimat

Kalimat adalah rangkaian fakta yang bisa dinilai benar atau salah (deklaratif). Jika tidak dapat dinilai benar atau salah, maka disebut tidak deklaratif.

• Contoh deklaratif: Haris adalah mahasiswa.

• Contoh tidak deklaratif: Kapan ujian dilaksanakan?

Jenis Kalimat

1. Kalimat sederhana → hanya satu nilai kebenaran.
   Contoh: Haris rajin.

2. Kalimat majemuk → lebih dari satu nilai kebenaran.
   Contoh: Haris rajin dan pandai.

3. Kalimat terbuka → mengandung variabel, nilainya belum pasti.
   Contoh: x > 5.

4. Kalimat tertutup → sudah jelas nilai kebenarannya.
   Contoh: Untuk semua x bilangan prima, x ≥ 3.

---

Logika

Logika adalah kaidah penalaran. Terdapat dua jenis:

• Deduktif: dari fakta umum → kesimpulan khusus.

  • Premis 1: Semua mahasiswa baru mengikuti OSPEK.

  • Premis 2: Haris adalah mahasiswa baru.

  • Kesimpulan: Haris mengikuti OSPEK.

• Induktif: dari fakta khusus → kesimpulan umum.

  • Premis: Ayam 1, Ayam 2, … Ayam 100 berkembang biak dengan bertelur.

  • Kesimpulan: Semua ayam berkembang biak dengan bertelur.

---

Logika Matematika

Disebut juga logika simbol, karena menggunakan simbol-simbol.

• Nilai kebenaran: Benar (B / 1) atau Salah (S / 0).

• Jika ada kata hubung → pernyataan majemuk.

• Jika tidak ada kata hubung → pernyataan sederhana.

---

Himpunan Semesta (S)

Himpunan = kumpulan elemen dalam suatu lingkup.

• Konstanta: elemen tetap.

• Variabel: peubah, bisa global/lokal.

• Simbol variabel: $x, y, z$ (angka), $p, q, r$ (kalimat).

---

Kalimat Terbuka

Kalimat yang mengandung variabel. Nilainya harus ditentukan dengan substitusi.

• Contoh: “x adalah bilangan bulat” → $x$ bisa 1, 2, 3, …

• Contoh himpunan: {Bil. Bulat}, {1,2,3,4}, {-4,-2,0,2,4}.

---

Negasi

Negasi = penyangkalan pernyataan dengan menambahkan kata tidak/bukan.

• Lambang: $-$, $\sim$, atau $!$.

• Contoh: p vs ¬p.

---

Pernyataan Majemuk

Pernyataan dengan kata hubung (konjungsi).

1. Konjungsi (∧) = “dan” → benar jika keduanya benar.

2. Disjungsi (∨) = “atau”

   • Inklusif (∨): benar jika salah satu atau keduanya benar.

   • Eksklusif (⊻): benar jika tepat satu benar.

3. Implikasi (⇒) = “jika … maka” → salah hanya jika anteseden benar tapi konsekuen salah.

4. Biimplikasi (⇔) = “bila dan hanya bila” → benar jika keduanya sama (benar/benar atau salah/salah).

Jika ada 3 pernyataan, kerjakan 2 lebih dulu, lalu gabungkan hasilnya dengan pernyataan ke-3.

 

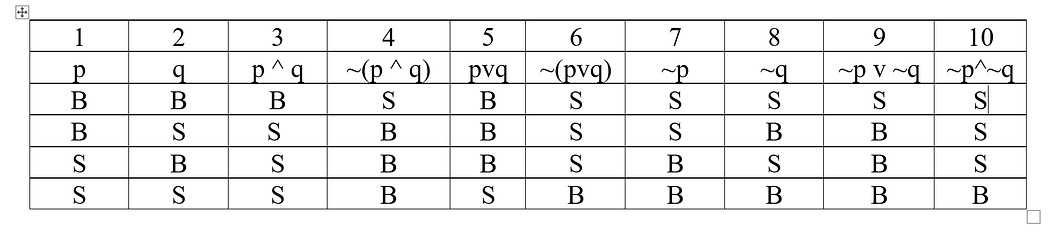
Tugas 1 |Soal No 1 di gabung dengan Soal no 2 

 ~Pengertian Konvers 

Konvers yaitu suatu pernyataan baru yang diambil dari implikasi (Pernyataan Asli) dengan cara di balik/menukar posisi.

Contoh: 

Implikasi> Jika Bapak Yasri Pria Maka Bapak Yasri Ganteng 

Konvers > Jika Bapak Yasri Ganteng Maka Bapak Yasri Pria

 ~Pengertian Invers 

Jika tadi konvers itu di balik/tukar posisi dari pernyataan asli (implikasi) sekarang invers, yaitu pernyataan yang menyangkal implikasi.

Contoh: 

Implikasi> Jika Bapak Yasri Pria Maka Bapak Yasri Ganteng 

Invers      > Jika Bapak Yasri Bukan Pria Maka Bapak Yasri Tidak Ganteng 

 ~Pengertian Kontraposisi 

Kontraposisi yaitu sebuah pernyataan yang ekuivalen dengan implikasi artinya jika sebuah pernyataan asli (Implikasi) benar maka Kontraposisi benar dengan syarat implikasi di balik dan di sangkal maka terbentuklah Kontraposisi.

Contoh: 

Implikasi > Jika Bapak Yasri Pria Maka Bapak Yasri Ganteng

Kontraposisi> Jika Tidak Ganteng Maka Bapak Yasri Bukan Pria

Tugas 2 

Tentukan kolom mana yang memiliki nilai kebenaran yang  sama !

Berikut Jawabannya: